Sphere Eversion

June 29, 2020

Topology is the study of the properties of geometric objects which aren’t changed by continuous deformation. A standard low-grade math joke is that toplogists consider a coffee mug and a doughnut equivalent because they’re both torii—(pauses for laughter)—one can be continuously deformed into the other, called a homeomorphism, without cutting or creasing the surface.

Homeomorphism between a doughnut and a mug. Source: Wikipedia

In this post, we play a topological game called eversion. Our objective is simple: turn a sphere inside out without cutting or creasing it. We consider a sphere, though a torus is also an interesting challenge.

That a sphere (specifically the two-sphere $S^2$ embedded in three dimensional space $\mathbb{R}^3$ ) can be turned inside out was proved by Stephen Smale in 1957. However the proof is a proof of existence, offering no particular guidance for those hoping to perform the feat.

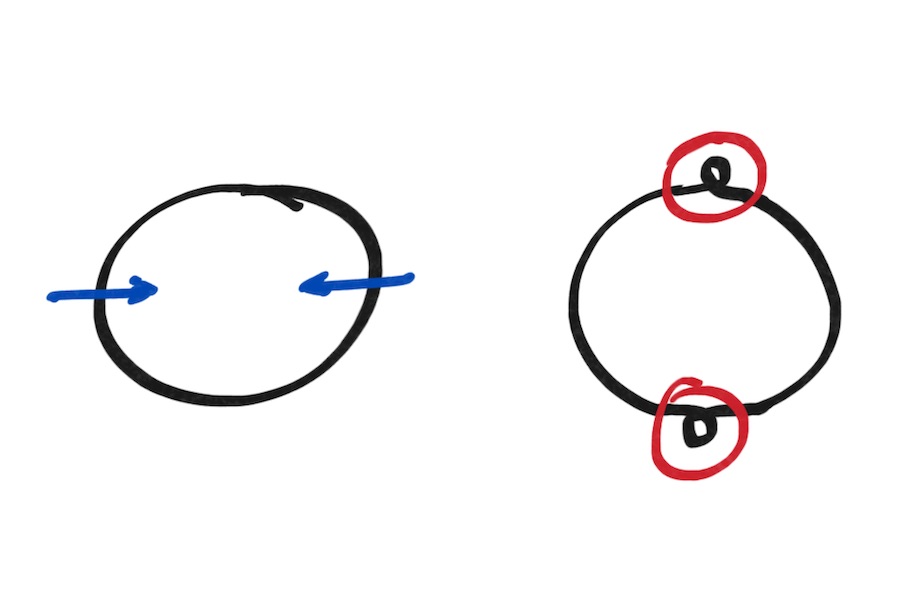
Circle eversion in two dimensions is impossible. We always get stuck!

We should take a moment to appreciate that the analogous problem of everting a circle in two dimensions is impossible. The figure above illustrates that there’s really nothing to do but introduce loops which we can’t then get rid of. Don’t take my word for it though! The classic video Outside In has an much more involved discussion of what happens when we try.

Since the original proof, a number of realizations of sphere eversion have been discovered, ranging in generality and complexity. This post follows the method of Bednorz and Bednorz from Analytic sphere eversion using ruled surfaces.

Before stepping through the eversion, we lay out our ground rules, of which there are just two: We may not cut the surface, and the surface must always remain smooth. Note that unlike physical objects, self-intersection is permitted.

Bednorz’ Sphere Eversion

We start with a full presentation of the sphere eversion of Bednorz and Bednorz in Analytic sphere eversion using ruled surfaces. It goes by quickly, so we’ll then break it down and try to understand it a bit better. Along the way, you can drag the slider at the top to examine cross-sections.

Quality:

We start with a sphere.

We push on one pole to form an indentation.

And add a bit of twist.

Here’s where the magic happens. We swap the inner and outer shells, being very careful not to introduce any creases.

Don’t worry! We’ll look at this step more carefully below.

Upon removing the indentation, we find the inside of the sphere has become the outside!

Success! But that all happened very quickly. What happens at the top is clearly the key. In some sense, we do simply push one end of the sphere right through the other, but we need some clever tricks to keep the hole at the top smooth.

Bednorz and Bednorz break down the method as follows. As long as nothing topologically interesting happens at the poles of the sphere, we can simply remove them from the equation and focus on a cylindrical band around the equator. All that’s left then is to manipulate the cylindrical band carefully and replace the poles at the end of the process.

The key element of their method is a family of ruled surfaces, or surfaces swept out by a straight line moving through space, which accomplish this task. They propose a family parameterized by time $t$ . They’re careful to prove the surface remains smooth during the process, but we’ll remain content to get to our destination and visually check the smoothness along the way.

They propose the family of ruled surfaces given by the equations

\begin{aligned} x &= t \cos \phi + p \sin (n - 1) \phi - h \sin \phi \\ y &= t \sin \phi + p \cos (n - 1) \phi + h \cos \phi \\ z &= h \sin n \phi - (t / n) \cos n \phi - qth. \end{aligned}

The variable $\phi$ parameterizes the polar angle of the cylinder from $-\pi$ to $\pi$ while $h$ parameterizes the vertical dimension of the cylinder. They suggest $q = 2/3$ and $p = 1 - |qt|$ .

Adjust the time parameter $t$ and observe the shape of the surface. There are two particular things to note. First, the surface always remains smooth, despite self-intersections, and second, the top and bottom of the edges of the cylinder swap places (with a bit of rotation which doesn’t trouble us) as we move from $t = -1.5$ to $t = 1.5$ .

Note also that although we’ll visualize eversion with $n = 2$ , the eversion also works for values greater than two.

t = 1.500000
n = 2

The proposed cylindrical ruled surface.

Of course we want to evert a full sphere and not just a cylindrical band, so the remainder of their paper focuses on using stereographic projections to smoothly close the caps of the cylindrical band and maintain the topology of the sphere during the entire process. The full eversion is illustrated above, but let’s now step back through it, taking a bit more care to focus on the region of interest.

We start again, this time with our perturbed sphere.

We restrict our attention to the cylindrical band separating the inner and outer shells.

As long as we keep the surface smooth and don’t twist the edges since we still have the rest of the sphere attached, we can distort the surface however we’d like.

To perform the eversion, we must swap the upper and lower edges of this cylinder.

Recall that we can’t just translate one end past the other without getting stuck with a cusp which violates our smoothness rule.

Let’s try again.

To avoid the cusp, we distort the cylinder into the above ruled surface with which we can smoothly swap the upper and lower edges.

We carefully slide one end past the other.

And remove the twist.

Restoring the poles which have been unaffected by the process, we confirm we’ve successfully turned our sphere inside out!

And that’s that! I regret that I have nothing novel or nuanced to say about the eversion itself, but my goal here was to explore the visual presentation since videos and images always left me wishing it were a bit more tangible.

There’s no shortage of really great visualizations and resources regarding sphere eversion, among other topics. Below are a few links relevant to both this eversion and the topic in general.

Analytic sphere eversion using ruled surfaces
Adam Bednorz Sphere Eversion: a webpage with videos and DIY instructions using paper!
Visualization by Marcel Padilla
Everting a Sphere by Chris Hills: an excellent collection of links and resources
Sphere Eversion on Wikipedia

This post is created using idyll and regl. You can find the full article source here.

Comments? Questions? Corrections? Let me know!