Projects
Observable Notebooks
A collection of Observable notebooks covering a wide range of topics and visualizations, spanning the gamut from half-baked experiements to detailed writeups.

eqn
An experimental equation parser which turns text like y = m * x + b into an Abstract Syntax Tree (AST) and then plugs into the Stdlib library to expose a wide variety of special math functions, at the end of the day wrapped up as a sort of drop-in replacement for Observable’s tex helper.

Night and Day
Using the CustomRasterSource API and Volodymyr Agafonkin’s SunCalc library to render a solar terminator on a Mapbox map.
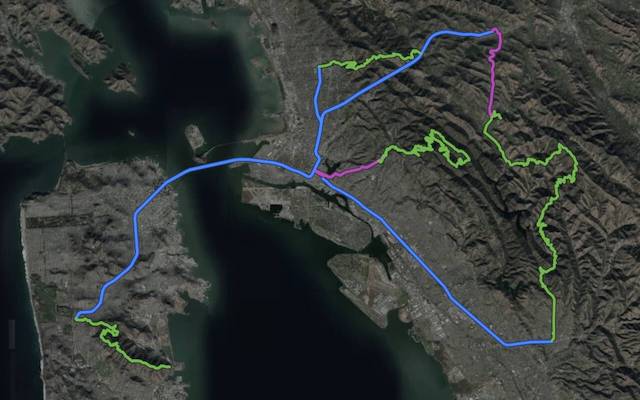
Trains and Trails
An interactive map-based exploration, In which I run Bay Area trails via public transportation.
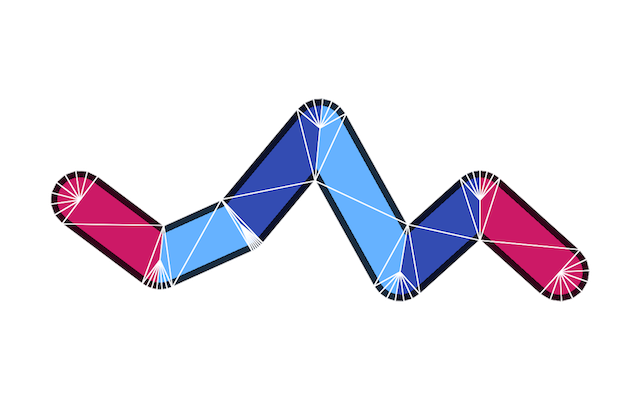
regl-gpu-lines
A small library to facilitate rendering vertex or texture data as lines using instanced rendering.

Strange Attractors on the GPU
A walkthrough of how to organize data on the GPU to iterate and render strange attractors as lines, without data leaving the GPU. See Part 1: Implementation and Part 2: Fun

Adaptive Contouring in Fragment Shaders
A detailed walkthrough of how to draw adaptively-scaled contours in a fragment shader without prior knowledge of the range of data.
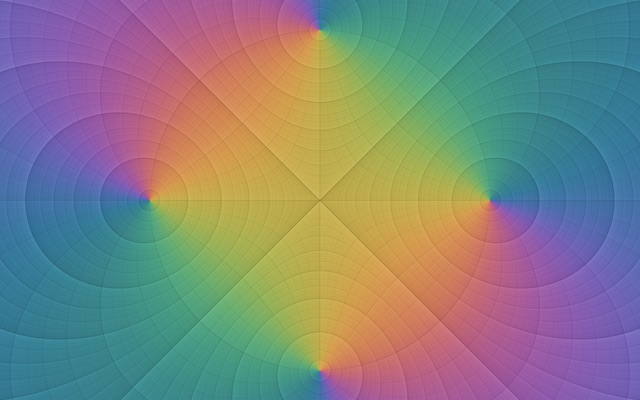
Complex Function Plotter
The n+1th iteration of my approach to domain coloring for complex functions, this time with a function parser to automatically turn a mathematical expression into GLSL code.
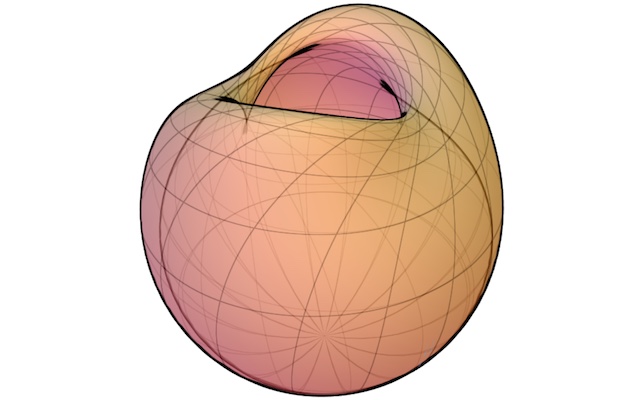
Sphere Eversion
While a circle in two dimensions cannot, a sphere in three dimensions can be smoothly turned inside-out! An interactive walkthrough to help visualize the eversion of Bednorz and Bednorz.

GPU Boids
Classic boids requires some sort of strategy for nearest-neighbor lookup, whether that’s a tree or brute-force pairwise interactions. This notebook follows a Particle Mesh method strategy and uses a grid to transmit locally averaged properties to neighboring boids.

Figure Reproduction: Monte-Carlo Geometry Processing
A reproduction of Figure 2 from Sawhney and Crane’s oustanding paper, Monte Carlo Geometry Processing. My very first foray into SDF rendering with sphere-tracing!

Toiletpaperfullerenes and Charmin Nanotubes
Toilet paper tubes have the curious property that you can flatten them, cut out loops, and link the loops together without fasteners. This notebook provides some instructions and implements a simple point and click editor to construct your own!

3D Reaction-Diffusion
A 3D WebGL simulation of Gray-Scott reaction-diffusion, implementing using two-dimensional WebGL 1 textures and a bit of clever bookkeeping.
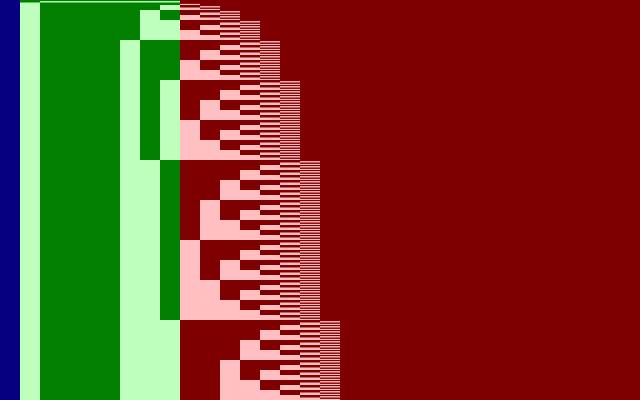
Integers in Single-Precision Floating-Point
You’re likely to get scolded for using a floating-point variable to represent an integer, but floating-point represents most integers perfectly well. Scroll through all of the integers representable in single-precision floating point!
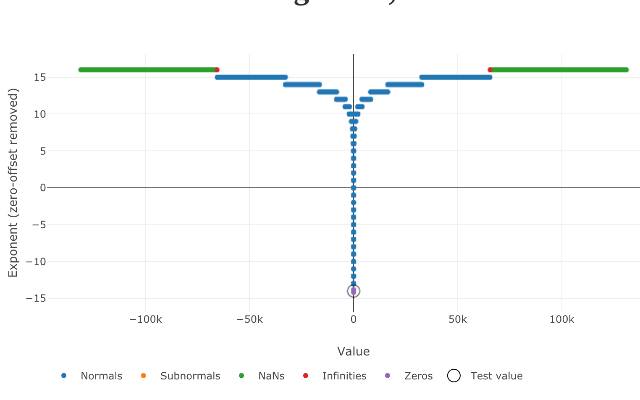
Half-Precision Floating-Point, Visualized
Half-precision floating-point can be surprisingly difficult to work with. This notebook plots all possible numbers with the special cases illustrated clearly.

Shadertoy: Adaptive Domain Coloring
A Shadertoy implementation of my domain coloring technique using rectangular contours or alternatively, polar contours.
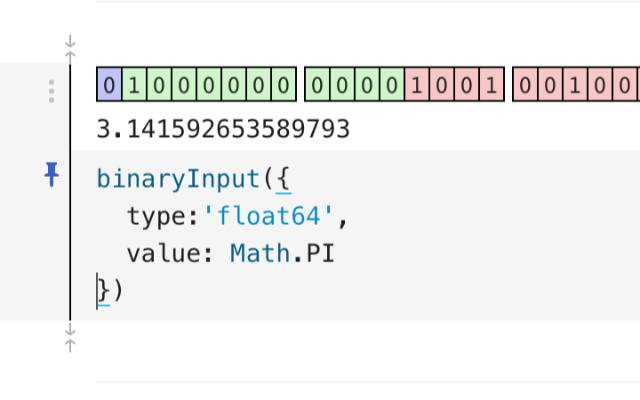
Binary Input
My favorite feature of Observable is the ease with which you can create surprisingly sophisticated ad-hoc user interfaces. This notebook implements an input field which allows you to toggle the bits of various numerical types.
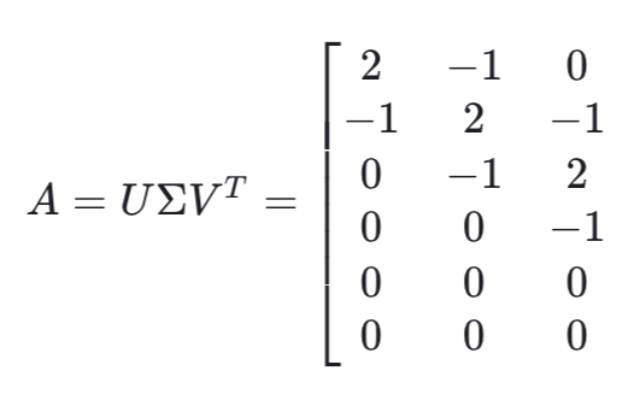
Linear Algebra via Eigen and WebAssembly: A proof of concept
Numerical computing in JavaScript remains difficult due to the lack of robust, complete libraries. This notebook explores compiling a subset of the Eigen linear algebra library to WebAssembly using Emscripten and tries to remedy some of the ergonomic memory management issues which result.
2D (Non-physical) N-body Gravity with Poisson’s Equation
N-body simulations get expensive very quickly, with the number of interactions growing with O(n2) . This notebook takes a shortcut and uses the somewhat inaccurate Particle-Mesh method to simulate 2D Newtonian gravity on a grid. It solves Poisson’s equation via an FFT and plots the results entirely on the GPU.
Periodic Planar Three-Body Orbits
This notebook collects over 2200 periodic, planar three-body orbits and explains one of the normal topological ways to classify them.

Finding Roots in the Complex Plane
Students of complex analysis will recall that a path integral quickly tells you how many roots are inside a given contour, but this notebook walks through the method of Delves and Lyness which transforms integrals around a contour into a polynomial whose roots are exactly the encircled roots!
Domain Coloring with Adaptive Contouring
Domain coloring for complex-valued functions is tricky since the function and rate of change may vary over many orders of magnitude. This notebook iterates on the previous technique and tries out automatic differentiation and screen-space derivatives to compute the rate of change and automatically scale contours.
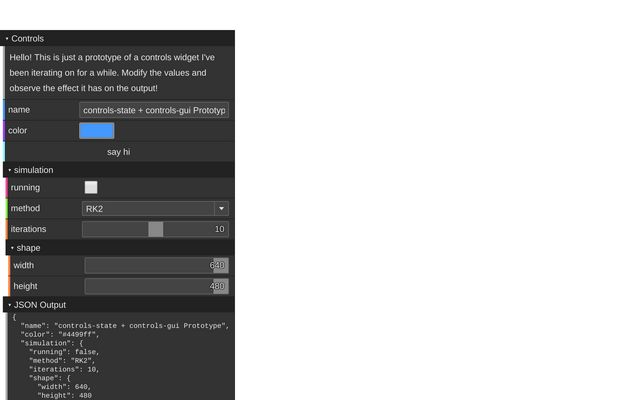
Control Panel Prototype
Dat.gui is the gold standard in simple control GUIs. This notebook illustrates a prototype libary based on Preact and with the goal of being simple and extensible.
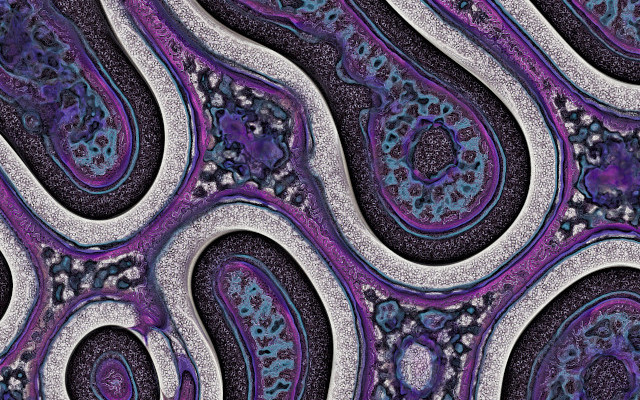
Multi-Scale Turing Patterns 2
A second set of multi-scale Turing patterns

Drawing indexed mesh data as screen-space normals without duplicating data
We typically just send triangles to the GPU and draw them on the screen. This notebook uses instanced rendering to draw plain, unadorned mesh data as normals with arrowheads and foreshortening.
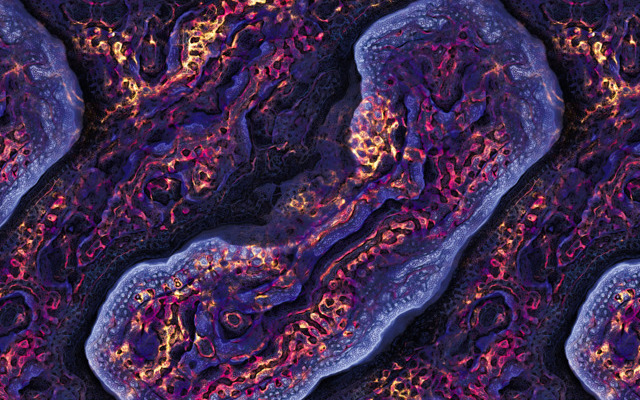
Multi-Scale Turing Patterns 1
An implementation of multi-scale Turing patterns following the method of Jonathan McCabe.
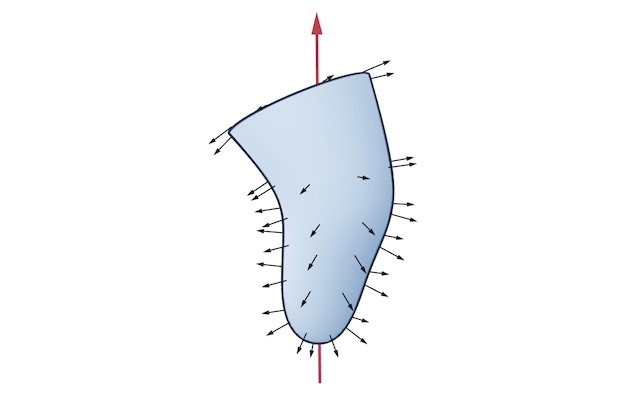
Aligning 3D scans
In which I have fun rediscovering Principal Component Analysis by stating what I want from a problem, realizing Lagrange multipliers actually work, then finding out it’s just Principla Component Analysis on the normal vectors.

From Nothing to Something in WebGL Using regl
A pretty good portion of the material on this site is implemented in WebGL using Mikola Lysenko’s oustanding regl library. This post walks through my still-favorite method of getting off of the ground in and into regl.

Things I Learned the Hard Way Using React Native
This post exists because I wish someone had sat me down and told me half of these things on Day One of using React Native.
A Series of Unfortunate Things I Programmed One Time
A walkthrough of how I got started and what motivates me to seek better ways to communicate.